palmerpenguins 데이터로 Classfication 예제 코드를 작성합니다. 이번 파트에서는
구성한 파이프라인(logistic regression)에 대해 분류 문제에서 사용되는 평가 지표에 대해 자세히 알아봅니다.
TL;DR
- multi-class 분류 문제의 경우, 평가 지표의 average 옵션을 활용할 수 있음.
- None: 각 class의 개별적인 지표값.
- ‘macro’: 각 class의 개별 지표의 평균값.
- ‘micro’: 전체 class에 대한 지표값.
1. 학습 및 예측
먼저, 지난 파트에서 진행한 전처리 과정까지 불러옵니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
from palmerpenguins import load_penguins
import numpy as np
import pandas as pd
from sklearn.pipeline import Pipeline
from sklearn.preprocessing import StandardScaler, OneHotEncoder
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LogisticRegression
from sklearn.compose import ColumnTransformer
penguins = load_penguins()
penguins = penguins.dropna(axis=0)
X_train = penguins[penguins.columns.difference(['species'])]
y_train = penguins['species']
X_train, X_test, y_train, y_test = train_test_split(X_train, y_train, random_state=42, test_size=0.4)
object_cols = X_train.select_dtypes('object').columns
num_cols = X_train.columns.difference(object_cols)
preprocessor = ColumnTransformer(
[
('scaler', StandardScaler(), num_cols),
('encoder', OneHotEncoder(handle_unknown='infrequent_if_exist'), object_cols),
]
)
다음으로 logistic regression 모델까지 파이프라인에 포함시킨 후 학습 및 예측을 진행합니다.
1
2
3
4
5
6
7
8
9
10
11
pipe = Pipeline(
[
('preprocessor', preprocessor),
('clf', LogisticRegression(random_state=42))
]
)
pipe.fit(X_train, y_train)
y_pred = pipe.predict(X_test)
y_proba = pipe.predict_proba(X_test)
2. 결과 지표 - precision, recall, F1-score
classification_report와 confusion_matrix를 통해 손쉽게 학습 모델의 성능을 확인할 수 있습니다.
1
2
3
4
from sklearn.metrics import classification_report, confusion_matrix, precision_score, recall_score, f1_score
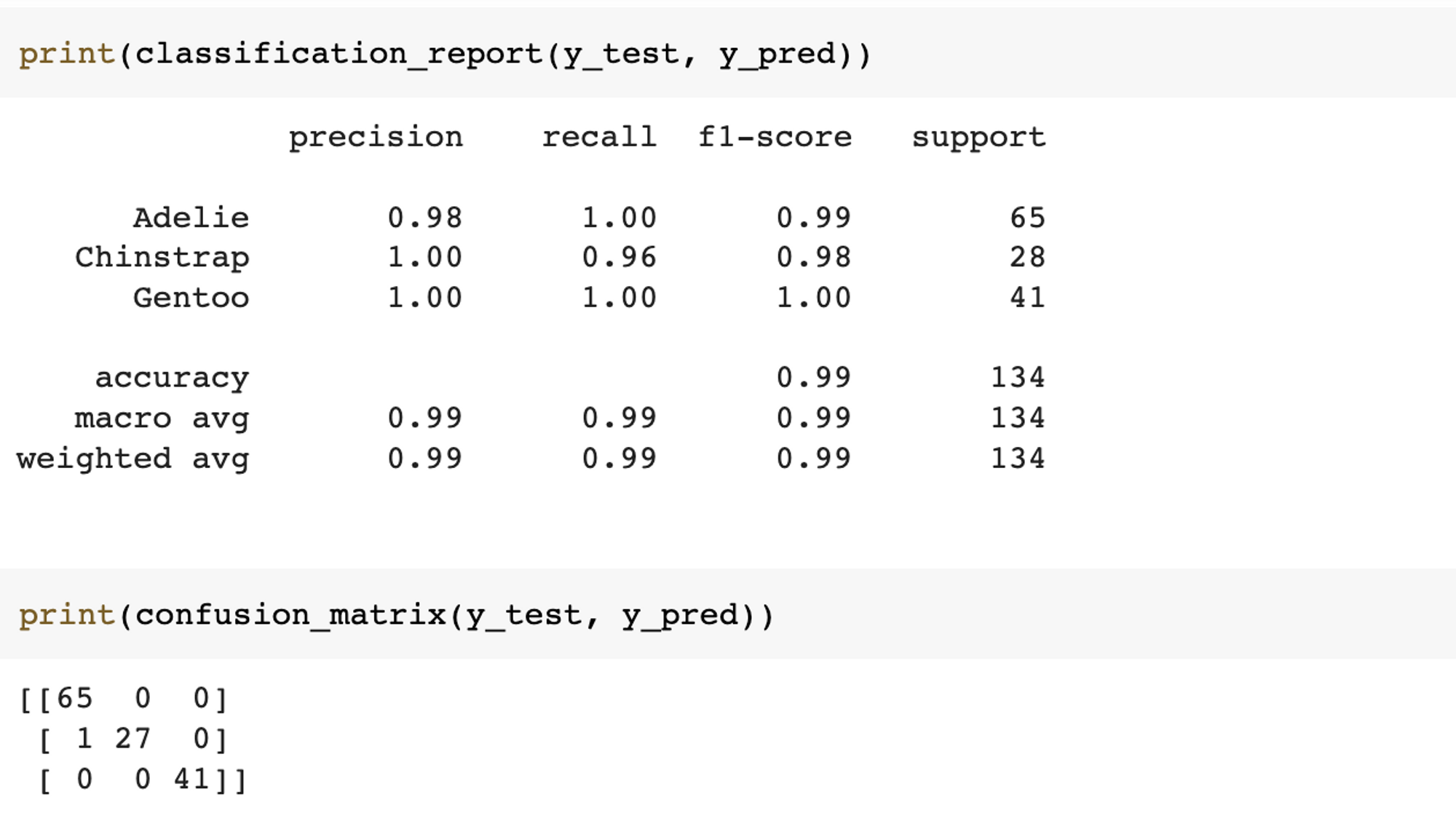
print(classification_report(y_test, y_pred))
print(confusion_matrix(y_test, y_pred))
예제에서 사용한 데이터는 multi-class 분류 문제이며, 그에 맞는 다양한 옵션을 알아 보겠습니다.
2.1 Precision
먼저 정확도(precision)입니다. 정확도는 아래와 같은 식으로 계산됩니다.
\[Precision = \frac{tp}{tp+fp}\]multi-class 분류 문제 지표들은 average옵션을 지원합니다. 각 옵션 별 자세한 내용은 다음과 같습니다. 첫 번째로 average=None인 경우, 각 class에 대한 precision 값을 출력합니다. 이전 confusion matrix를 통해 첫 class의 tp(true positive)은 65이고 fp(false positive)는 1인 것을 알 수 있습니다. 이를 통해 precision을 계산하면 average=None으로 했을 때 첫 class의 결과인 0.984848이 계산됩니다.
1
2
3
4
5
6
7
print(precision_score(y_test, y_pred, average=None))
# [0.98484848 1. 1. ]
tp = 65
fp = 1
tp / (tp + fp)
# 0.9848484848484849
두 번째로 average='macro'인 경우입니다. 해당 옵션은 모든 class의 개별적인 precision의 전체 평균값입니다. average=None으로 계산된 값의 평균을 통해 해당 값을 확인할 수 있습니다.
1
2
3
4
5
6
# precision - macro
print(precision_score(y_test, y_pred, average='macro'))
# 0.9949494949494949
precision_score(y_test, y_pred, average=None).mean()
# 0.9949494949494949
세 번째로 average='micro'인 경우입니다. 해당 옵션은 각 class의 개별적인 성능을 계산하지 않고 globally하게 통합적인 precision 값을 제공합니다. 이전 confusion matrix를 통해 전체 tp는 133(=65+27+41)이며, 전체 fp는 1인 것을 알 수 있습니다. 이 값을 통해 precision을 계산하면 0.992537이며, average='micro'일 때의 결과값이 계산됨을 확인할 수 있습니다.
1
2
3
4
5
6
# precision - micro
print(precision_score(y_test, y_pred, average='micro'))
# 0.9925373134328358
(65+27+41) / (65+27+41+1)
# 0.9925373134328358
2.2 Recall
다음으로 재현율(recall)입니다. 재현율은 아래와 같은 식으로 계산됩니다.
\[Recall = \frac{tp}{tp+fn}\]1
2
3
4
5
6
7
print(recall_score(y_test, y_pred, average=None))
# [1. 0.96428571 1. ]
tp = 27
fn = 1
tp / (tp + fn)
# 0.9642857142857143
2.3 F1-score
마지막으로 F1-score입니다. F1-score는 아래와 같은 식으로 계산됩니다.
\[Recall = \frac{2}{1/precision + 1/recall} = \frac{2*precision*recall}{precision + recall}\]1
2
3
4
5
6
7
8
print(f1_score(y_test, y_pred, average=None))
# [0.99236641 0.98181818 1. ]
prec_lb1 = precision_score(y_test, y_pred, average=None)[0]
recall_lb1 = recall_score(y_test, y_pred, average=None)[0]
2*(prec_lb1*recall_lb1)/(prec_lb1 + recall_lb1)
# 0.9923664122137404
3. 마무리
몇 가지 참고할 내용으로 이번 part를 마무리 하겠습니다.
- multi-class 분류 문제의 경우, 데이터가 푸는 문제의 상황(imbalanced label, 각 class의 틀렸을 때 비용이 다름 등)에 따라 적절한 average 옵션을 이용해야 함.
- 위에서 얘기한 지표들 이외에 Youden’s J index, F-beta score 등 문제 상황에 따라 확인할 수 있는 다른 지표들도 있음.