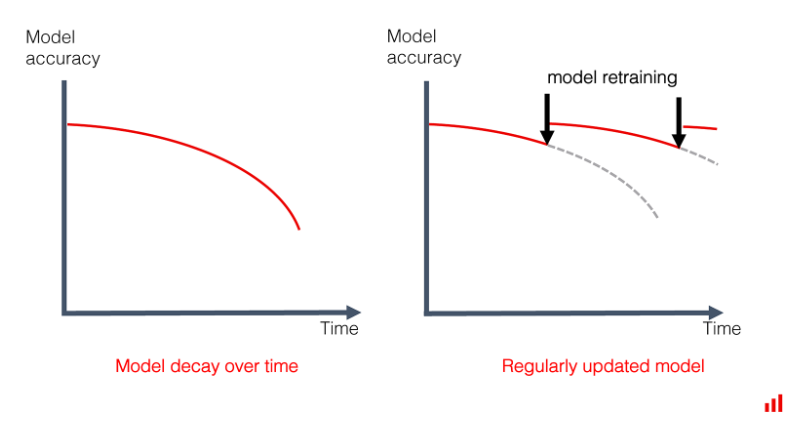
ML이나 DL 모델을 개발해 이용하면 시간이 지날수록 모델의 성능이 감소합니다. 모델 개발 시점의 우리는 훈련 데이터와 테스트 데이터의 분포가 같음을 가정하고 모델을 개발합니다. 하지만 시간이나 외부 환경이 점진적으로 또는 갑자기 변화하는 것은 매우 자연스러운 현상입니다. 이런 상황에서 데이터의 특성은 언제든 변할 수 있으며, 개발한 모델을 계속 사용할 수 있을지를 결정하기 위해 모니터링이 필요합니다. 여기서 필요한 개념인 ‘Model Drift’에 대해서 알아보겠습니다.
Model Drift?
 출처: EVIDENTLY AI - Machine Learning Monitoring, Part 5: Why You Should Care About Data and Concept Drift
출처: EVIDENTLY AI - Machine Learning Monitoring, Part 5: Why You Should Care About Data and Concept Drift
‘Model Drift’란 시간과 환경의 변화에 따라 모델의 성능이 낮아지는 것을 의미합니다. 조금 더 자세히 살펴보면 시간이나 주변 환경의 변화에 따라 데이터의 특성이 바뀌게 되고 이로 인해 ‘피쳐(설명변수, 독립변수)와 타겟(반응변수, 종속변수) 간의 관계’ 또는 ‘피쳐 간의 관계’가 달라집니다. 이러한 관계의 변화로 인해 개발 당시의 데이터 정보 만을 갖고 있는 모델의 성능이 낮아지게 되는 것입니다.
Model Drift 종류
1. Concept Drift
‘Concept Drift’는 타겟과 피쳐 간의 관계 변화로 인한 Model Drift를 말합니다. 즉, 두 시점 $t1, t2$ 에 대해,
\[P_{t1}(Y |X) \ne P_{t2}(Y|X)\]인 경우를 말합니다. 이러한 현상은 타겟 변수의 의미가 바뀌는 경우 발생할 수 있습니다. 예를 들면, 신용평가모형에서 우불량 기준이 변경되는 경우 등이 있습니다. 이렇게 타겟의 의미가 변하면 기존 피쳐의 영향도가 변경되게 되고 타겟에 대한 피쳐의 설명력이 감소하게 됩니다.
2. Data Drift
‘Data Drift’는 피쳐의 특성(통계값, 분포 등) 변화로 인한 Model Drift를 말합니다. 즉 두 시점 $t1, t2$ 에 대해,
\[P_{t1}(X) \ne P_{t2}(X)\]인 경우를 말합니다. 이러한 현상은 계절적 요인이나 피쳐의 의미 변화 등으로 인해 발생할 수 있습니다. 예를 들면, 코로나 발생으로 인한 고객의 행동 데이터가 변화하거나 특정 고객의 세그먼트의 정의가 달라지는 경우가 있습니다.
3. 기타
이외에도 위 두 개념과 동일/유사한 개념으로 Label Drift, Prediction Drift, Feature Drift 등이 있습니다.
How to detect Model Drift?
Model Drift를 탐지하는 방법으로는 크게 ‘Model에 기반한 방법’과 ‘통계 검정에 기반한 방법’이 있습니다.
1. Continuous evaluation
Continuous evaluation이란 새롭게 생성되는 n개의 데이터를 이용해 모델의 성능을 지속적으로 모니터링하며 미리 정의한 threshold 이상의 성능인지를 확인하는 방법입니다.
여기에서는 ‘얼마나 자주 모델을 평가할 것인지’와 관련해
고정된 time interval마다 확인할 지
정해진 수의 데이터가 모였을 때 확인할 것인지
를 결정해야 합니다.
2. Population Stability Index (PSI)
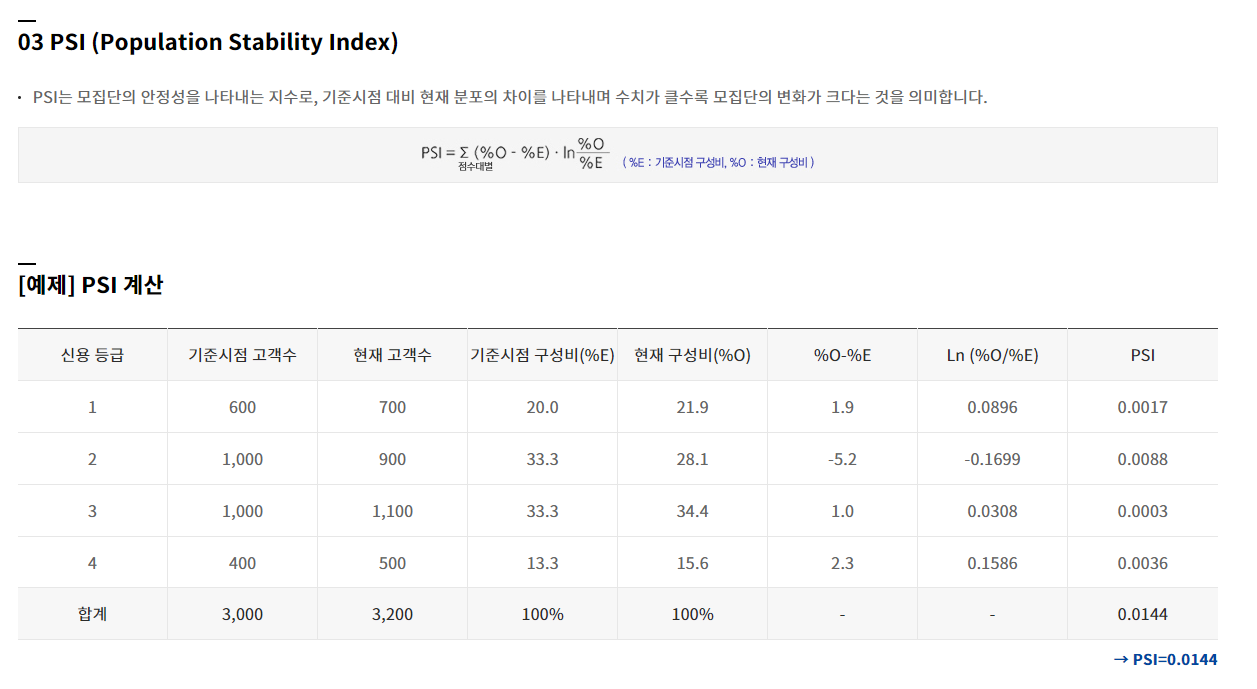
PSI는 모델 개발 시점의 데이터와 현재 데이터 간 분포가 얼마나 다른지를 구성비를 통해 비교하는 방법입니다. 연속형 자료일 경우에는 10개 혹은 20개 정도의 구간으로 구분하여 구성비를 계산합니다. 계산하는 식은
\[PSI = \sum ((\%O - \%E) \times \log(\frac{\%O}{\%E}))\]이며, $\%O$는 현재 데이터의 구성비, $\%E$는 개발 데이터의 구성비를 의미합니다.
PSI를 판단하는 일반적인 기준(Rule of thumb, 절대적인 기준은 아님)은 다음과 같습니다.
- PSI $\lt$ 0.1 : 변화없음(No change)
- 0.1 $\le$ PSI $\lt$ 0.1 : 약간의 변화(Slight Change)
- 0.1 $\le$ PSI : 유의미한 변화 (Significant change)
참고로, PSI는 데이터의 차이를 판별하는 특성을 이용해 신용평가 분야에서 모집단의 안정성(개발시점과 현재시점의 차주 구성의 차이)을 나타내는 지수로 모형 평가에 활용됩니다.
3. Kullback-Leibler Divergence
Kullback-Leibler Divergence는 통계나 정보이론 분야에서 사용되는 두 확률분포의 차이를 계산하는 측도입니다. KL-Divergence의 정의는 아래와와 같습니다.
\[D_{KL}(P||Q)=\int log(\frac{p(x)}{q(x)}) p(x) dx = \mathbb{E}[log({p(x)}) - log({q(x)})]\]Kullback-Leibler Divergence는 다음과 같은 2가지 특징이 있습니다.
$D(P||Q) \ge 0 \quad \& D(P||Q) = 0$ iff $P = Q$ (nonnegative)
$D(P||Q) \ne D(Q||P)$ (asymmetric)
특히 ‘2’와 같은 특징으로 인해 KL-Divergence는 거리 개념으로 사용할 수 없습니다. 참고로, Jensen-Shannon Divergence는 KL-Divergence를 통해 계산할 수 있으며 symmetric 성질을 만족합니다. Jensen-Shannon Divergence의 정의는 아래와 같습니다.
\(JSD(P||Q) = \frac{1}{2} D(P||M) + \frac{1}{2}D(Q||M)\) 여기서 $M = \frac{1}{2}(P+Q)$ 입니다.
4. Kolmogorov-Smirnov test
통계학에서 두 분포가 동일한지를 검정하기 위한 비모수적 통계검정 방법입니다. Empirical (Cumulative) Distribuion $F_n(x)$와 검정통계량 $D_n$은 다음과 같습니다.
$F_n(x) = \frac{1}{n} \sum_{i=1}^{n} 1_{(-\infty,x]}(X_i)$이며
$1_{(-\infty,x]}$은 $X_i \le x$ 이면 1 그렇지 않으면 0의 값을 가지는 indicator 함수입니다.
$D_{n,m} = sup_{x}|F_{1,n}(x) - F_{2,m}(x)|$
마무리
Model Drift의 signal이 관측되었다면 바로 모델을 재학습해야 할까? 그렇지 않다. 우선, Drift가 발생한 근본적인 원인을 파악해야 한다. 실제로 Drift가 발생한 것인지, 아니면 Data를 Injection하는 과정에서 문제가 있는 것인지 Data Quality에 대한 체크를 해야 한다. 또한 Drift가 실제로 발생했다 하더라도 재학습에 필요한 충분한 데이터가 모였는지, 모델 외적인 방법으로 해결할 수 있는지 등 여러 조건을 고려하며 의사결정을 해야 하겠다.